Decision Tree Learning in Ruby
 You've built a vibrant community of Family Guy enthusiasts. The SVD recommendation algorithm took your site to the next level by allowing you to leverage the implicit knowledge of your community. But now you're ready for the next iteration - you are about to roll out some new opt-in customizations, but you don't want to bug every user by asking them if they want to participate. And so it occurred to you: "wouldn't it be nice if we could just ask a subset of our users, and then extrapolate this knowledge to predict the preferences for the rest?"
You've built a vibrant community of Family Guy enthusiasts. The SVD recommendation algorithm took your site to the next level by allowing you to leverage the implicit knowledge of your community. But now you're ready for the next iteration - you are about to roll out some new opt-in customizations, but you don't want to bug every user by asking them if they want to participate. And so it occurred to you: "wouldn't it be nice if we could just ask a subset of our users, and then extrapolate this knowledge to predict the preferences for the rest?"
And once again, machine learning comes to the rescue! Except this time, it will be a decision tree. Whether you're trying to solve a marketing problem, building a medical diagnosis system, or trying to learn the preferences of a user, this technique can do wonders.
Decision trees: what, where, and why
Decision trees fall into the category of inductive machine learning algorithms. Given a set of examples (training data) described by some set of attributes (ex. age, marital status, education) the goal of the algorithm is to learn the decision function stored in the data and then use it to classify new inputs. Let's work through an example:
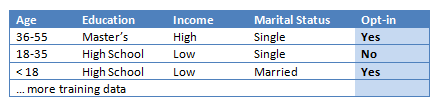
For the full training dataset take a look at Christopher Roach's article. His data is for a slightly different application, but we can easily translate this problem into the context of our Family Guy community. Feeding all of the examples into the algorithm, and graphing the resulting tree gives us:
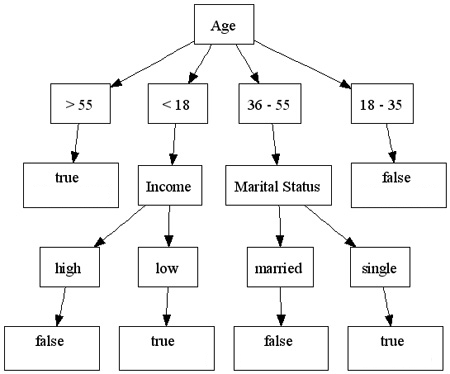
Our dataset contains four different attributes, but our decision tree shows that only three make a difference! In this case, 'education' appears to be irrelevant to the final opt-in decision. Intuitively, we could build a tree which contains every attribute by simply providing a path for every training example, but is that the best we can do? Instead, we want to eliminate attributes which serve as weak predictors (education) - we want to compress the data, and that is exactly what a decision tree algorithm will do. Given a set of examples, and a list of attributes, a decision tree algorithm tries to find the smallest tree that is consistent with the examples. As a bonus, the output of the algorithm can be automatically graphed and interpreted visually - a rare occurrence in the machine learning field. In other words, don't be surprised if all of the sudden the VP of marketing becomes your best buddy!
Understanding information gain
 We swept some of the details of the underlying algorithm under the rug, but they're worth a closer look. In order to build our decision tree, we need to be able to distinguish between 'important' attributes, and attributes which contribute little to the overall decision process. Intuitively, the most important attribute should go at the top of the tree because it carries the most information. Likewise for the second attribute, third, and so forth. But how do we quantify 'important'?
We swept some of the details of the underlying algorithm under the rug, but they're worth a closer look. In order to build our decision tree, we need to be able to distinguish between 'important' attributes, and attributes which contribute little to the overall decision process. Intuitively, the most important attribute should go at the top of the tree because it carries the most information. Likewise for the second attribute, third, and so forth. But how do we quantify 'important'?
Thankfully, Claude Shannon and Warren Weaver have already done most of the work for us in their 1949 publication: Model of Communication. Specifically, they provided a formula to measure the numbers of bits required to encode a stream of data. Thus, first we can measure the number of bits that our entire training set requires, and then we can repeat this procedure to measure the number of bits each attribute can provide us. Intuitively, the attribute which will yield the most information should become our first decision node. Then, the attribute is removed and this process is repeated recursively until all examples are classified. For the mathematically inclined, this procedure can be translated into the following steps:
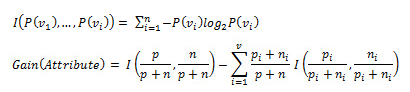
As you may have guessed, I(a,b) measures the amount of information. First, the formula calculates the information required to classify the original dataset (p - # of positive examples, n - # of negative examples). Then, we split the dataset on the selected attribute (with v choices) and calculate the information gain. This process is repeated for every attribute, and the one with the highest information gain is chosen to be our decision node. Of course, there is a reason why we swept this stuff under the rug in the first place. Instead of worrying about the math, you can simply make use of my freshly minted gem: decisiontree. Install it, and we are ready to go: sudo gem install decisiontree
Learning discrete datasets (classification)
When working with discrete datasets (separate and distinct attribute labels), we are trying to solve a classification problem. Let's take a look at how we can do this in Ruby:
require 'rubygems'
require 'decisiontree'
attributes = ['Age', 'Education', 'Income', 'Marital Status']
training = [
['36-55', 'Masters', 'High', 'Single', 1],
['18-35', 'High School', 'Low', 'Single', 0],
['< 18', 'High School', 'Low', 'Married', 1]
# ... more training examples
]
# Instantiate the tree, and train it based on the data (set default to '1')
dec_tree = DecisionTree::ID3Tree.new(attributes, training, 1, :discrete)
dec_tree.train
test = ['< 18', 'High School', 'Low', 'Single', 0]
decision = dec_tree.predict(test)
puts "Predicted: #{decision} ... True decision: #{test.last}";
# Graph the tree, save to 'discrete.png'
dec_tree.graph("discrete")Note that the last field in the training set specifies the label for that example (opt-in or not). You can also find the full example of the sample tree we discussed above bundled with the source of the gem. In order to graph the tree, you will need Graphviz and GraphR libraries installed on your system.
Learning continuous datasets (regression)
Regression, or learning datasets with continuous attributes (temperature, height, etc.) is also supported by the decisiontree gem. In fact, the interface is remarkably similar:
require 'rubygems'
require 'decisiontree'
# Medical diagnosis based on chemical tests
attributes = ['K', 'Na', 'Cl', 'Endotoxin']
training = [
[4.6, 138, 102, 27.5, 1],
[4.5, 141, 103, 26.5, 1],
[3.2, 139, 98, 30.7, 0]
# ... more training examples
]
# Instantiate the tree, and train it based on the data (set default to '1')
dec_tree = DecisionTree::ID3Tree.new(attributes, training, 1, :continuous)
dec_tree.train
test = [3.2, 144, 105, 24.4, 0]
decision = dec_tree.predict(test)
puts "Predicted: #{decision} ... True decision: #{test.last}";You will also find a full dataset and implementation of a decision tree regression bundled with the source code - this one is for medical diagnosis!
And that's it, now we're ready to roll our next batch of updates with some (artificial) intelligence. This almost makes me wonder: what machine learning wonder will our Family Guy enthusiasts see next?
In other iterations: SVD Recommendation System, Bayes Classification, Support Vector Machines
 Ilya Grigorik is a web ecosystem engineer, author of High Performance Browser Networking (O'Reilly), and Principal Engineer at Shopify — follow on
Ilya Grigorik is a web ecosystem engineer, author of High Performance Browser Networking (O'Reilly), and Principal Engineer at Shopify — follow on