Scalable Datasets: Bloom Filters in Ruby
When you're working with large datasets it's always nice to have a few algorithmic tricks up your sleeve, and Bloom Filters are exactly that - often overlooked, but an extremely powerful tool when used in the right context. A Bloom Filter is a probabilistic data structure that is used to test whether an element is a member of a set, or more simply, it's an incredibly space efficient hash table that is often used as a first line of defense in high performance caches. Database queries too expensive? Then a Bloom Filter might help. As an example, Google's Bigtable uses a bloom filter as first lookup to avoid unnecessary disk accesses.
Bloom Filter theory and Applications
Instead of storing the key-value pairs, as a regular hash table would, a Bloom filter will give you only one piece of information: true or false based on the presence of a key in the hash table (equivalent to Enumerable's include?() function in Ruby). This relaxation allows the filter to be represented with a much smaller piece of memory: instead of storing each value, a bloom filter is simply an array of bits indicating the presence of that key in the filter. Trying to build a fast spellchecker? Bloom filters are your best friend.
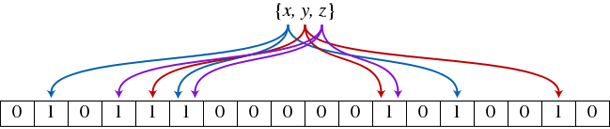
The 'probabilistic' part of the filter comes from the fact as with any Hash table, there is a probability of collision where two keys may map into the same bucket. Hence, false positives are possible (a filter with a single entry ('word') may indicate that ('word2') is part of the set, but the reverse (false-negatives) are not possible).
The possibility of a false-positive is something you'll have to deal with (for most caches it doesn't matter, since Bloom filters are an optimization technique to guard against the expensive operations), but as with any probability we can optimize it for each use case (speed vs error rate). For this exact reason, Bloom filters often use multiple hash functions for each key. Let's see what that means...
Understanding the Math
Wikipedia has a great explanation of the math behind Bloom Filters, which I would encourage you to walk through, but the takeaway is that the probability of a false-positive (where k is the number of hashing functions, n is the size of the set, and m is the size of the bloom filter in bits) is:
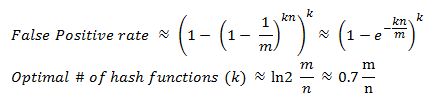
Hence, we can pick a desired error rate and optimize the size of the filter to match our requirements. In fact, if you do the math, you'll find an interesting rule of thumb: a Bloom filter with a 1% error rate and an optimal value for k only needs 9.6 bits per key, and each time we add 4.8 bits per element we decrease the error rate by ten times. Let's see what that means in practice for a 10,000 word dictionary:
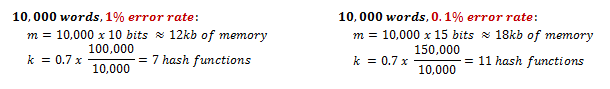
0.1% error rate for a 10,000 word dictionary in 18kB of memory? Not bad! Now let's do it Ruby.
Working with Bloom Filters in Ruby
After some poking around I've resurrected Tatsuya Mori's sbloomfilter, fixed a few bugs, and extended the library. To create the filter, you'll have to specify the size of the filter (m), the number of hash functions (k), and a random seed:
#!/usr/bin/env ruby
require 'bloomfilter'
WORDS = %w(duck penguin bear panda)
TEST = %w(penguin moose racooon)
# m = 100, k = 4, seed = 1
bf = BloomFilter.new(100, 4, 1)
WORDS.each { |w| bf.insert(w) }
TEST.each do |w|
puts "#{w}: #{bf.include?(w)}"
end
bf.stats
# penguin: true
# moose: false
# racooon: false
#
# Number of filter bits (m): 100
# Number of filter elements (n): 4
# Number of filter hashes (k) : 4
# Predicted false positive rate = 0.05%bloomfilter-rb.git - Ruby Bloom Filter implementation
Once the filter is populated you can easily view the stats and expected error rate. Current limitations are: the hash function is fixed as CRC32 and seeded with k different values, and currently you cannot delete entries from a Bloom Filter - for that, a counting Bloom filter must be implemented. Go forth and conquer!
Ilya Grigorik is a web ecosystem engineer, author of High Performance Browser Networking (O'Reilly), and Principal Engineer at Shopify — follow on Twitter.